对数的由来或者对数的起源相关的视频或者啥的,对数函数的由来历史
本文目录
1.对数函数的由来历史 2.试述对数视力表的原理 3.对数的由来,起源及发展 4.自然对数e的来历
对数函数的由来历史
16世纪末至17世纪初的时候,当时在自然科学领域(特别是天文学)的发展上经常遇到大量精密而又庞大的数值计算,于是数学家们为了寻求化简的计算方法而发明了对数.德国的史提非(1487-1567)在1544年所著的《整数算术》…

试述对数视力表的原理
对数的起源 对数产生于以加减运算代替乘除运算的探索中.
以加(减)代乘(除)的想法早就存在了.一个简单的三位数乘法(例如265×438),一般需要四次运算才能得出结果,但同样数字的加法却只需一次运算.涉及的数字越大,则乘(或除)所需要的运算次数比加(或减)所需的运算次数相差得越多.因此,在6世纪以前,就曾有人作尝试,试图实现以加(减)代乘(除).但由于压力不大,并不感到非如此不可,因此未能达到目的.
16世纪中叶,由于天文和航海而引起的大数计算日益激增,这种计算不仅花去了人们大量的精力,而且难以精确,于是,以加(减)代乘(除)的设想再次被提出,并被作为必须解决的问题加以考虑了.
起初,曾采用以下两个公式来实现乘除向加减的转化:
但由于它们都需要通过另一种运算(三角或平方)来实现转化,并不真正地提高效率,所以很快就被搁置不用了.
能不能使乘(除)直接向加(减)转化呢?能!1484年,法国数学家舒开(Chuquet,?—1500)通过把等差数列与等比数列,如:
0,1,2,3,4,… 等差 1,2,4,8,16,… 等比
或0,1,2,3,4,… 等差 1,3,9,27,81,… 等比
比较发现:等比数列中任何两项的积,可以用与这两项序号对应的等差数列的和来表示(注:这一点最早由阿基米德发现).由于当时舒开并不力图解决这个问题,因此他仅提出了这个发现,而没加以深入地研究.
半个世纪后,同样的事实再次被德国数学家史提非提出.史提非以如下一组数列为例指出:“等比数列中数的乘、除、乘方、开方可以转化为等差数列中数的加、减、乘、除来实现.”如4×8,因为4和8对应的等差数列的数分别是2和3,而2+3=5,所以4×8的结果是5所对应的等比数中的数32.又如82,因为8对应的等差数列中的数是3,3×2=6,所以82的结果是6所对应的等比数列中的数64.就这样,史提非轻巧地实现了运算的转化,并且他意识到:“只要把这个思想进一步发挥,那么必定能得出关于数的性质的全新的论述.”遗憾的是史提非后来再也没进行深入的研究,他放弃了进一步发挥思想的权利,因而也就失去了对数发明者的资格.布尔基与耐普尔 数学史册上的对数发明者是两个人:英国的约翰·耐普尔(John Naeipr,1550-1617)和瑞士的乔伯斯特·布尔基(Jobst Bürgi,1552-1632).
布尔基原是个钟表技师,1603年被选为布拉格宫庭技师后,开始与著名的天文学家开普勒接触,了解到天文学计算的一些具体情况.他体察天文学家的辛劳,并决定为他们提供简便的计算方法.
布尔基所提出的简便计算方法就是一张实用的对数表.从原则上说,史提非已经解决了将乘(除)运算转为加(减)运算的途径.但是史提非所给出的两个数列中的数字十分有限,它不能付之于实用,实用的对数表必须包括所有要乘的数在内.
为了做到这一点,布尔基采取尽可能细密地列出等比数列的办法.他给出的等比数列相当于: 1,1.0001,(1.0001)2,(1.0001)3,…,(1.0001)104,…
其相应的等差数列是:0,0.0001,0.0002,0.0003,…,1,…
这里,等差数列中的1,对应于等比数列中的(1.0001)104.就是说,布尔基在造表时,把对数的底取为(1.0001)104=2.71814593…,与自然对数的底e=2.718281828…相差不远.但需要的指出是,无论是布尔基还是后面要讲到的耐普尔,他们都没有关于对数“底”的观念.因为他们都不是从ax=N的关系出发来定义对数x=logaN的.
耐普尔原是苏格兰的贵族.生于苏格兰的爱丁堡,十二岁进入圣安德鲁斯大学的斯帕希杰尔学院学习.十六岁大学尚未毕业时又到欧洲大陆旅行和游学,丰富了自己的学识.耐普尔虽不是专业数学家,但酷爱数学,他在一个需要改革计算技术的时代里尽心尽力.正如他所说:“我总是尽量使自己的精力和才能去摆脱麻烦而单调的计算,因为这种令人厌烦的计算常使学习者望而生畏.”耐普尔一生先后为改进计算得出了球面三角中的“耐普尔比拟式”、“耐普尔圆部法则”以及作乘除用的“耐普尔算筹”,而为制作对数表他花了整整20年时间.
1614年,耐普尔发表了他的《关于奇妙的对数表的说明》一书,书中不仅提出数学史上的第一张对数表(布尔基的对数表发表于1620年),而且阐述了这个发明的思想过程.他说:假定有两个质点P和Q,分别沿着线段AZ和射线A'Z'以同样的初速运动,其中Q保持初速不变,而P作减速运动,其速度与这个点离Z的距离成正比,现在,如果当P位于某点B时,Q位于B',那么,A'B'就是BZ的对数!同样的A'C'是CZ的对数,等等(图 1).建立了这个模型以后,耐普尔通过代入具体的数字得出BZ、CZ、DZ、EZ、FZ…一系列数值为:
,…
以及作为它们的对数的A'B',A'C',A'D',A'E',A'F',…一系列数值为: 1,2,3,4,5,…显然,这也是一组相互对应的等比数列和等差数列,因此耐普尔实质是把等差数列中的数定义为对应的等比数列中的数的对数!这说明,耐普尔借助于质点运动建立起来的对数概念,其原理仍不外乎等比数列与等差数列关系的合理运用.

对数的由来,起源及发展
16世纪末至17世纪初的时候,当时在自然科学领域(特别是天文学)的发展上经常遇到大量精密而又庞大的数值计算,于是数学家们为了寻求化简的计算方法而发明了对数。

16世纪末至17世纪初的时候,当时在自然科学领域(特别是天文学)的发展上经常遇到大量精密而又庞大的数值计算,于是数学家们为了寻求化简的计算方法而发明了对数。
德国的史提非(1487-1567)在1544年所着的《整数算术》中,写出了两个数列,左边是等比数列(叫原数),右边是一个等差数列(叫原数的代表,或称指数,德文是Exponent ,有代表之意)。
欲求左边任两数的积(商),只要先求出其代表(指数)的和(差),然后再把这个和(差)对向左边的一个原数,则此原数即为所求之积(商),可惜史提非并未作进一步探索,没有引入对数的概念。
自然对数e的来历
自然对数:以常数e为底数的对数叫做自然对数记作ln N(N>0).
欧拉(Leonhard Euler ,1707-1783) 著名的数学家,瑞士人,大部分时间在俄国和法国度过.他17岁获得硕士学位,早年在数学天才贝努里赏识下开始学习数学,毕业后研究数学,是数学史上最高产的作家.在世发表论文700多篇,去世后还留下100多篇待发表.其论著几乎涉及所有数学分支. 著名的七座桥问题也是他解决的。 他是创立数学符号的大师。首先使用f(x)表示函数,首先用∑表示连加,首先用i表示虚数单位.1727年首先引用e来表示自然对数的底。 欧拉公式有两个 一个是关于多面体的 如凸多面体面数是F顶点数是V棱数是E则V-E+F=2这个2就称欧拉示性数。 另一个是关于级数展开的 e^(i*x)=cos(x)+i*sin(x). 这里i是虚数单位i的平方=-1。
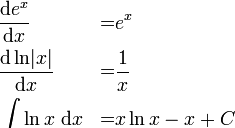
当x趋近于正无穷或负无穷时,[1+(1/x)]^x的极限就等于e,实际上e就是通过这个极限而发现的。它是个无限不循环小数。其值约等于2.718281828…
它用e表示
以e为底数的对数通常用于㏑
而且e还是一个超越数
e在科学技术中用得非常多,一般不使用以10为底数的对数。以e为底数,许多式子都能得到简化,用它是最“自然”的,所以叫“自然对数”。
涡形或螺线型是自然事物极为普遍的存在形式,比如:一缕袅袅升上蓝天的炊烟,一朵碧湖中轻轻荡开的涟漪,数只缓缓攀援在篱笆上的蜗牛和无数在恬静的夜空携拥着旋舞的繁星……
螺线特别是对数螺线的美学意义可以用指数的形式来表达:
φkρ=αe
其中,α和k为常数,φ是极角,ρ是极径,e是自然对数的底。为了讨论方便,我们把e或由e经过一定变换和复合的形式定义为“自然律”。因此,“自然律”的核心是e,其值为2.71828……,是一个无限不循环数。
“自然律”之美
“自然律”是e及由e经过一定变换和复合的形式。e是“自然律”的精髓,在数学上它是函数:
(1+1/x)^x
当X趋近无穷时的极限。
人们在研究一些实际问题,如物体的冷却、细胞的繁殖、放射性元素的衰变时,都要研究
(1+1/x)^x
X的X次方,当X趋近无穷时的极限。正是这种从无限变化中获得的有限,从两个相反方向发展(当X趋向正无穷大的时,上式的极限等于e=2.71828……,当X趋向负无穷大时候,上式的结果也等于e=2.71828……)得来的共同形式,充分体现了宇宙的形成、发展及衰亡的最本质的东西。
现代宇宙学表明,宇宙起源于“大爆炸”,而且目前还在膨胀,这种描述与十九世纪后半叶的两个伟大发现之一的熵定律,即热力学第二定律相吻合。熵定律指出,物质的演化总是朝着消灭信息、瓦解秩序的方向,逐渐由复杂到简单、由高级到低级不断退化的过程。退化的极限就是无序的平衡,即熵最大的状态,一种无为的死寂状态。这过程看起来像什么?只要我们看看天体照相中的旋涡星系的照片即不难理解。如果我们一定要找到亚里士多德所说的那种动力因,那么,可以把宇宙看成是由各个预先上紧的发条组织,或者干脆把整个宇宙看成是一个巨大的发条,历史不过是这种发条不断争取自由而放出能量的过程。
生命体的进化却与之有相反的特点,它与热力学第二定律描述的熵趋于极大不同,它使生命物质能避免趋向与环境衰退。任何生命都是耗散结构系统,它之所以能免于趋近最大的熵的死亡状态,就是因为生命体能通过吃、喝、呼吸等新陈代谢的过程从环境中不断吸取负熵。新陈代谢中本质的东西,乃是使有机体成功的消除了当它自身活着的时候不得不产生的全部熵。
“自然律”一方面体现了自然系统朝着一片混乱方向不断瓦解的崩溃过程(如元素的衰变),另一方面又显示了生命系统只有通过一种有序化过程才能维持自身稳定和促进自身的发展(如细胞繁殖)的本质。正是具有这种把有序和无序、生机与死寂寓于同一形式的特点,“自然律”才在美学上有重要价值。
如果荒僻不毛、浩瀚无际的大漠是“自然律”无序死寂的熵增状态,那么广阔无垠、生机盎然的草原是“自然律”有序而欣欣向荣的动态稳定结构。因此,大漠使人感到肃穆、苍茫,令人沉思,让人回想起生命历程的种种困顿和坎坷;而草原则使人兴奋、雀跃,让人感到生命的欢乐和幸福。
e=2.71828……是“自然律”的一种量的表达。“自然律”的形象表达是螺线。螺线的数学表达式通常有下面五种:(1)对数螺线;(2)阿基米德螺线;(3)连锁螺线;(4)双曲螺线;(5)回旋螺线。对数螺线在自然界中最为普遍存在,其它螺线也与对数螺线有一定的关系,不过目前我们仍未找到螺线的通式。对数螺线是1638年经笛卡尔引进的,后来瑞士数学家雅各·伯努利曾详细研究过它,发现对数螺线的渐屈线和渐伸线仍是对数螺线,极点在对数螺线各点的切线仍是对数螺线,等等。伯努利对这些有趣的性质惊叹不止,竟留下遗嘱要将对数螺线画在自己的墓碑上。
以上就是关于对数的由来或者对数的起源相关的视频或者啥的,对数函数的由来历史的全部内容,以及对数的由来 的相关内容,希望能够帮到您。
















