什么是复功率?它如何把视在功率、有功、无功有机的结合在一起?
大家好,我是犹如雨下。今天我们来谈一谈电路中复功率是什么?
复功率?什么是复功率?咋一听朋友你是不是有许多问号?其实复功率的概念很简单,它是为了我们方便进行电路计算而人为设置的一个计算量。
我们来看一看这样一个简单的电路,在如图所示的一端口电路中,端口电压是正弦交流电uS来表示,端口电流用正弦交流电is来表示。在正弦电路中我们常用向量的形式来表示电压和电流,就是U和I。
现在我们这样定义这样一个电流I*,它的复数表达形式是:
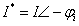
共轭电流的相量表达式
我们把这样一个电流I*命名为共轭电流。
现在我们来看一看什么是复功率,我们把复功率定义为如下形式:S=UI*
我们把复功率展开来看一下,看看复功率身上藏着什么奥秘?
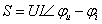
复功率表达式
过对复功率的展开我们发现一个奥秘,那就是复功率中含有一个这样我们熟悉的量,那就是ψu-ψi我们来回顾一下这个量代表的是什么,这个量代表的就是功率因数角,就是阻抗角。
所以复功率Š可以用如下的形式来表示既Š=UI∠θ。这个θ就是电路中的功率因数角,就是阻抗角。
我们现在进一步深入了解复功率Š这个物理量,把复功率Š展开成复数的形式,我们会发现复功率Š另外的一个奥秘。
Š=UIcosθ+jUIsinθ
在复功率的代数表达式中实部UIcosθ就是有功功率P的数学表达式、虚部UIsinθ就是无功功率的数学表达式。
这样我们发现我们就可以用有功功率P、无功功率Q来表示复功率Š
Š=P+jQ
复功率的模值可以用∣Š∣=√P2+Q2,我们发现复功率的模值就是视在功率S!
也就是说复功率可以用有功功率P和无功功率 Q来表示这样我们就找到了视在功率Š的奥秘所在。在正弦交流电路中我们常用相量的形式来表示电压、电流。为了能用相量直接计算出有功功率P、无功功率Q,我们定义了复功率Š的概念。
定义复功率Š=UI*=UI∠ψu-ψi=UI∠θ,这样我们就可以利用电压、电流的有效值以及阻抗角(也是功率因数角)很快求解出有功功率P、无功功率Q、视在功率S。电压有效值、电流有效值可以用电流变、电压表、万用表直接测量,阻抗角可以通过有效的手段间接的得到,这样电路中的这三种功率就很清晰、简单的得到!
实际上复功率Š并没有什么实际的物理含义,这是作为一个方便表示有功功率P、无功功率Q、视在功率S的人为定义出的一个量。
接下来我会出一个视频举一个简单的电路实例来进行复功率计算的实际演练。欢迎大家在今日头条和西瓜视频观看。
今天的分享就到这里,我们下期再见!
犹如雨下
2020.05.10于马鞍山风电场