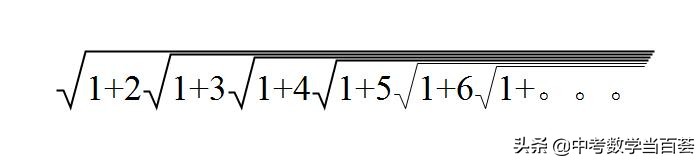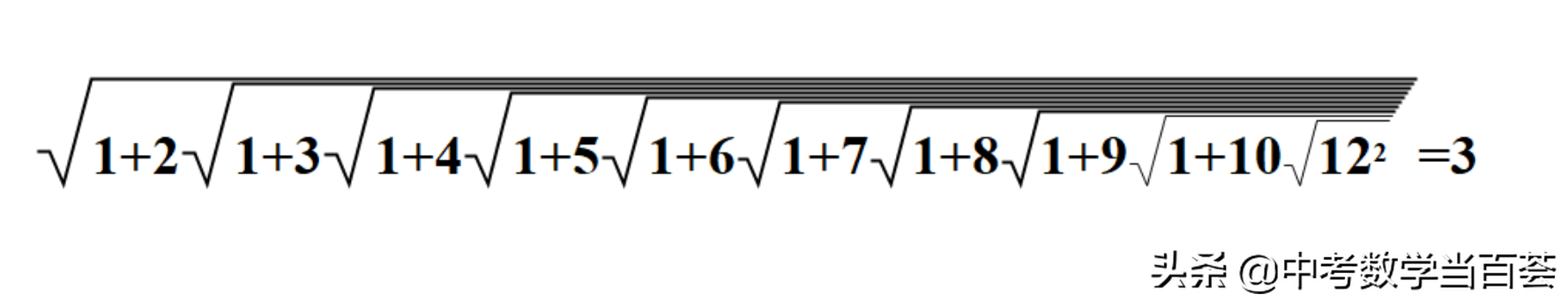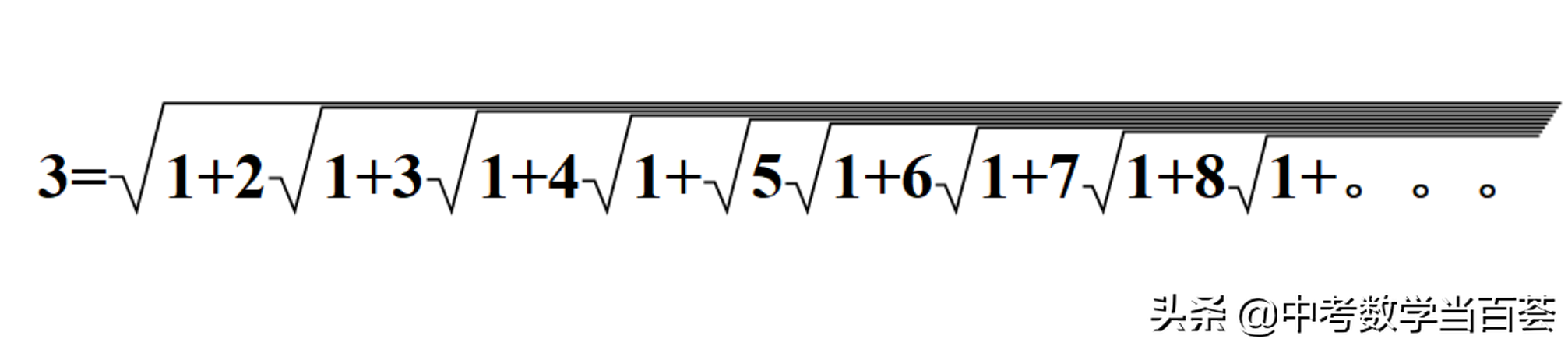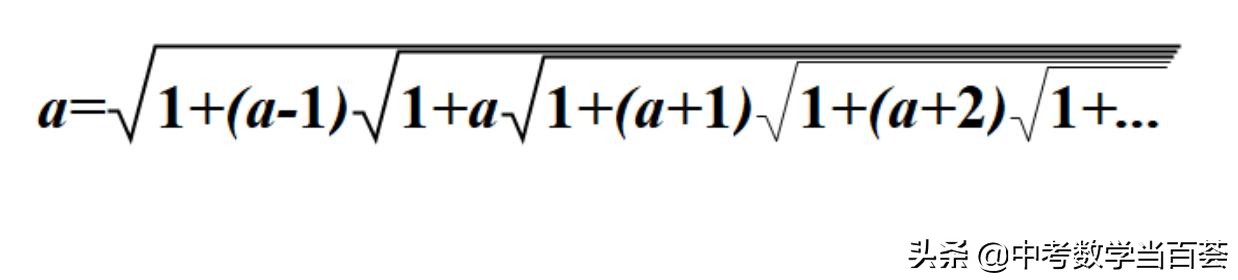拉马努金公式大全（拉马努金恒等式，一个初中生能看懂并能证明的神奇公式）
拉马努金公式大全（拉马努金恒等式，一个初中生能看懂并能证明的神奇公式）
-01-拉马努金恒等式
2016年4月8日在英国上映了一部名叫《知无涯者》的电影。电影讲述了印度数学家斯里尼瓦瑟·拉马努金（1887.12.22~1920.4.26），
短暂而传奇的一生。拉马努金出生贫寒，没有受过专门的数学训练，但天资聪颖，完全靠自学。直到1913年，得到英国数学家哈代的赏识，他的数学才华大放异彩。但他不同于传统意义上数学家，他的成果往往是凭直觉得到，只有结论，而没有证明。他短暂的一生发现了3900条数学公式和命题，许多结果完全是新颖的、原始的和非传统的，但被后续证明他的结论都是正确的。
本文要介绍的这个恒等式，就是拉马努金流传最广的成果之一。先看这个恒等式的一边：
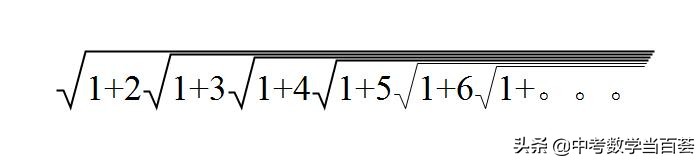
我相信大多数人能按照这个式子的规律接着写下去，但会发现这是无穷尽的，并且很好奇这个式子的结果到底是多少？
拉马努金说，这个式子的结果等于3。
他对形如
上式的
无穷二次根式，进行深入研究得到这个结果，并且将此发表在《印度数学会刊》上征集证明，数月内无人能应。
-02-拉马努金恒等式的数学逻辑
下面我们以今天中学生的认知来看其中的数学逻辑：
3=√9。。。。。一层根号
=√1+8
=√1+2×4
=√1+2√16。。。。二层根号
=√1+2√1+15
=√1+2√1+3×5
=√1+2√1+3√25。。三层根号
=√1+2√1+3√1+24
=√1+2√1+3√1+4×6
=√1+2√1+3√1+4√36。四层根号
。。。。。。
由此不难发现：将3拆分后，含n层根号时，3=
√1+2√1+。。。n√（n+2）²
。。。n层根号
验证一下，n=10时（由外向内数，含10层根号），壮观景象：
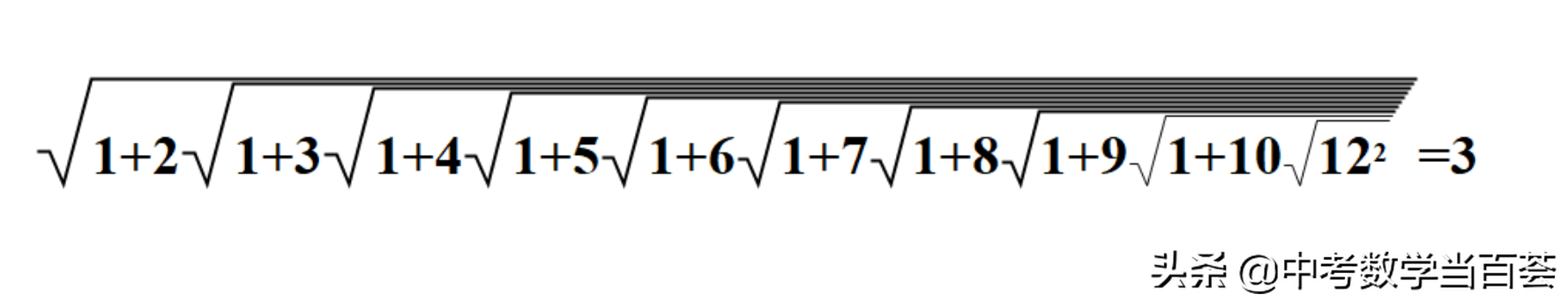
第10层根号里的数：
12²=144；
第9层根号里的数：
11²=121；
第8层根号里的数：
10²=100；
。。。
第3层根号里的数：
5²=25；
第2层根号里的数：
4²=144；
第1层根号里的数：
3²=9；
√9=3
理所当然是个恒等式。
-03-拉马努金恒等式的数学证明
问题来了，正整数3可以象这样用二次根式进行无穷拆分，那么其他正整数呢？他是怎么想到了呢？
平方差公式是初中代数中的最基本的公式之一：
a²-1=(a-1)(a+1)；
变形得
a²=1+(a-1)(a+1)；
即
a=√1+(a-1)(a+1)。
建立一个关于a的函数：
F（a）=a=√1+(a-1)(a+1)，则
F（a+1）=a+1
=√1+(a+1-1)(a+1+1)
=√1+a(a+2)
=√1+aF(a+2)，
F（a+2）=a+2
=√1+(a+2-1)(a+2+1)
=√1+(a+1)(a+3)
=√1+(a+1)F(a+3),
F（a+3）=a+3
=√1+(a+3-1)(a+3+1)
=√1+(a+2)(a+4)
=√1+(a+2)F(a+4)，
…
F（a+n）=a+n
=√1+(a+n-1)(a+n+1)
=√1+(a+n-1)F(a+n+1)，
…
通过层层嵌套，得到
F(a)=√1+(a-1)F(a+1)
=√1+(a-1)√1+aF(a+2)
=√1+(a-1)√1+a√1+(a+1)F(a+3)
…
=√1+(a-1)√1+a√1+(a+1)√1+(a+2)√1+。。。
即
其中，a为正整数。
当a=2时，得到
当a=3时，得到
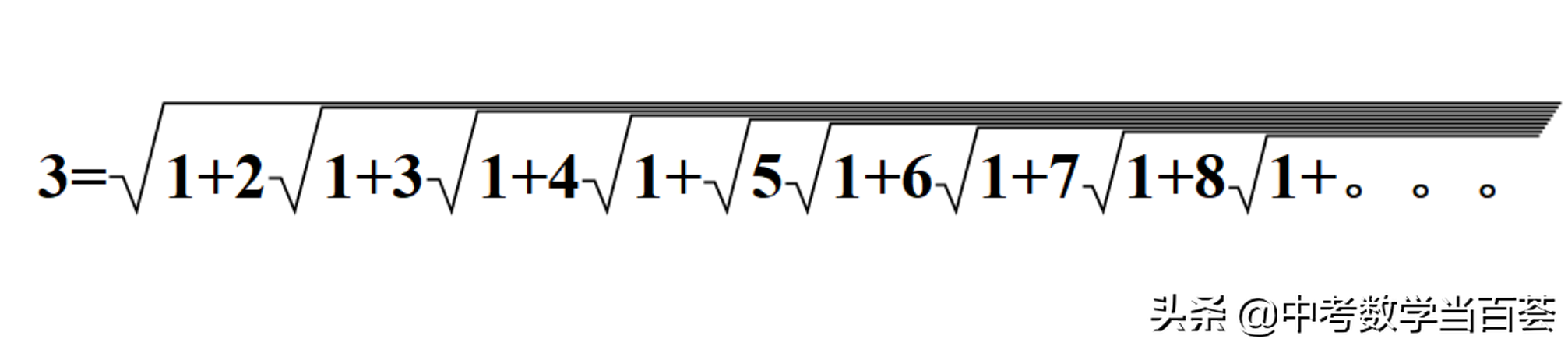
当a=4时，得到
由此，可以把任意一个正整数，用二次根式有规律地无穷展开。
所以拉马努金恒等式，更一般的形式是：
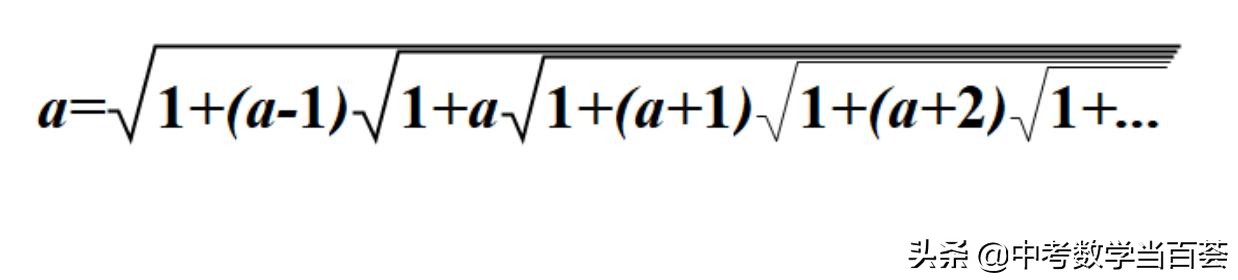
-04-结语
利用平方差公式和函数嵌套（复合函数）的思想，可以来说明他的正确性。虽然初中不提函数嵌套（复合函数）这种说法，但“整体思想”已经具备其雏形，所以上述证明过程，数学程度稍好的同学也可以看懂。
拉马努金没有受过正规的高等数学教育，但他靠自学沉湎于数论，尤其钟爱涉及π、质数等数学常数的求和公式和整数分拆。特别是他对数的直觉（数感）常常令人称奇，以至于亦师亦友的哈代感叹说：“我们学习数学，拉马努金则发现并创造了数学。”
标签：
179
哪个牌子的眼霜好用(5款热门好用的“大牌眼霜”：欧莱雅性价比高，娇韵诗提亮 淡纹) 不管是年轻肤质还是轻熟龄肌，眼霜的使用都是越早越好的。 对于眼部的黑眼圈和细纹问题，眼...
75
口罩的原材料是什么（口罩最核心的材料——熔喷布 你了解多少？） 近期， 新冠肺炎疫情蔓延全球，口罩成为紧缺物资。防护用口罩的加工离不开口罩面料，而口罩面料中最核心的就...
129
北京开车注意事项（在北京开车需要注意什么） 今年五一放5天假，假期有点多啊，话又说回来了，想去大城市来个自驾该怎么办呢，今天就详细的介绍在北京开车需要注意的事情。 一...
65
三不沾是什么 嘿嘿，你吃过“三不沾”吗？ 告诉大家一个“小秘密”，小编是一枚资深吃货！ 早上吃什么？中午吃什么?晚上吃什么?都是一直困扰着小编的问题… 身在北京，当然是去...
81
卓尔不群褒义还是贬义 导语： 体育界也好，各行各业也罢；作为决策者，切莫压抑人的个性。凤雪君认为，凡个性鲜明者，或从众心理弱（或曰自我约束力差），会使他人感到不舒服...
180
宫商角羽下一句是什么? 30句学写对联歌诀，背下来 古人学对联歌诀集锦 平对仄，仄对平。平仄两分明。有无与虚实，死活并重轻。上去入声皆仄韵，东西南字是平声。虚对实，实对虚...
160
米诺地尔酊真的可以生发吗（用米诺地尔能生发、防脱？是真的，但没这么简单） 在双十一、双十二期间，健康类型消费也成了一匹黑马。其中关于防脱发的产品，深受人们的喜爱。尤...
173
薄荷叶的功效与作用（化解暑气 驱散身体） 1、我们在饮用含有薄荷成分的饮料时能兴奋大脑、促进血液循环、发汗，可以用于解暑解热。 2、薄荷里面含有薄荷醇等因子，会让人的皮...
200
vap是什么意思？如何诊治？来看最新专家共识 血管性 帕金森综合征（VaP）是继发性帕金森综合征中较为常见的一种类型，是在脑血管疾病及其相关病理因素的基础上发展而来的，具有...
67
ps牙齿美白小技巧（Photoshop用这两种方法速效美白牙齿技巧，让你再也不怕遇 上大黄牙了） 一般形容人美漂亮，会用唇红齿白、明眸皓齿这样的词汇，其中都提及了牙齿，说明牙齿的亮...
138
自考有哪些专业选择(自学考试十大热门专业选择推荐) 自学考试专业怎么选？其实很多考生在选择自考专业时都比较纠结，不知道选择什么专业好， 一、管理类专业 1、行政管理 课程内...
163
上古四大凶兽 四凶分别是： 饕餮 、 混沌 、 梼杌 和 穷奇 。以人为食，所过之处往往尸骨遍地，寸草不生，天灾人祸不断，而且行为举止残暴，因此被封为四大凶兽。 饕餮 饕餮的样...
184
卢森堡大公是元首吗（至今统治卢森堡的朝代——拿骚王朝历代大公真容，全是俊 男和美女） 随着现代历史发展，君主制似乎已经渐行渐远，因此仍然实行君主制的国家在某种意义上...
78
羽毛球拍购买注意事项（想打羽毛球不知道怎么选拍，看这里，一文告知） 在羽毛球比赛的战场中，球拍就是我们的武器，一款合适的羽毛球拍，可以帮助你在赛场上发挥出自己的水平...
155
延边朝鲜族自治州属于哪个省（市县地名溯源：延吉·边疆——延边） 延边朝鲜族自治州位于吉林省东部，是吉林省惟一的少数民族自治州。“延边”这个名称是在“延吉”这一地名出...
193
蟋蟀吃什么才能养活(蟋蟀的人工养殖技术) 蟋蟀能量棒 蟋蟀干燥虫体入药，性温，味辛咸，有毒，功能利尿，主治水肿、小便不通。人工养殖蟋蟀不失为致富冷门。 1.饲养设备 蟋蟀可...
165
泸州世家浓香型38度(泸州世家42度价格) 泸州世家浓香型38度白酒，采用泸州老窖传统工艺酿造，酒体醇厚丰满，入口绵柔，回味悠长，空杯留香持久。这款酒的价格在200元左右，适合家...
120
macallan怎么喝(MACALLAN什么酒) Macallan是一款来自苏格兰的名酒，是世界上最受欢迎的威士忌之一。如果你还没有品尝过这款佳酿，你可能会觉得不知道如何喝这种酒。事实上，Macallan的品...
164
泸州醇两瓶装多少钱 泸州醇42度价格6瓶装 泸州醇两瓶装多少钱？泸州老窖特曲是中国四大名酒之一，也是浓香型白酒的典型代表，其历史悠久，品质优良，深受消费者喜爱。泸州老窖...
65
黄鹤楼酒是清香型白酒(黄鹤楼清香型白酒45度v3) 黄鹤楼酒是清香型白酒，酒体清澈透明，入口绵甜爽净，回味悠长，具有独特的酱香风格。黄鹤楼酒的生产工艺采用传统酿造工艺，在原...