勾股定理证明方法(我国最出名的勾股定理证明方法)
来源:数学教育(ID:mathedu01); 作者:丁前鹏
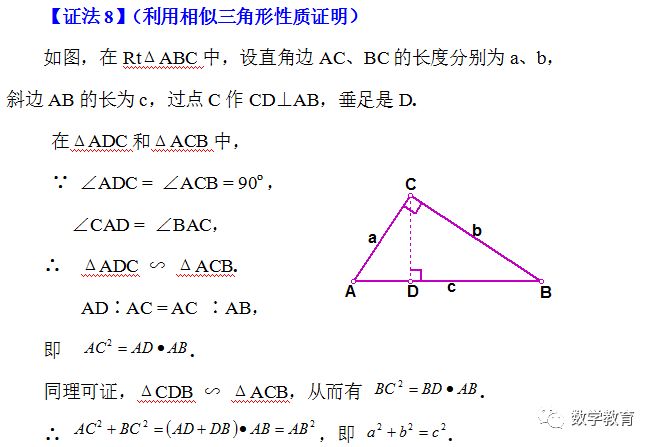
【证法1】(课本的证明)
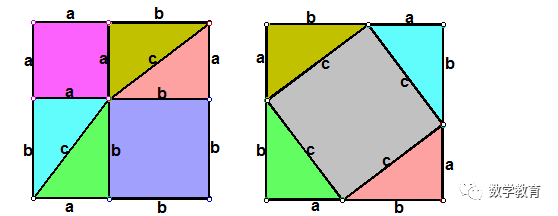
做8个全等的直角三角形,设它们的两条直角边长分别为a、b,斜边长为c,再做三个边长分别为a、b、c的正方形,把它们像上图那样拼成两个正方形.
从图上可以看到,这两个正方形的边长都是a + b,所以面积相等. 即

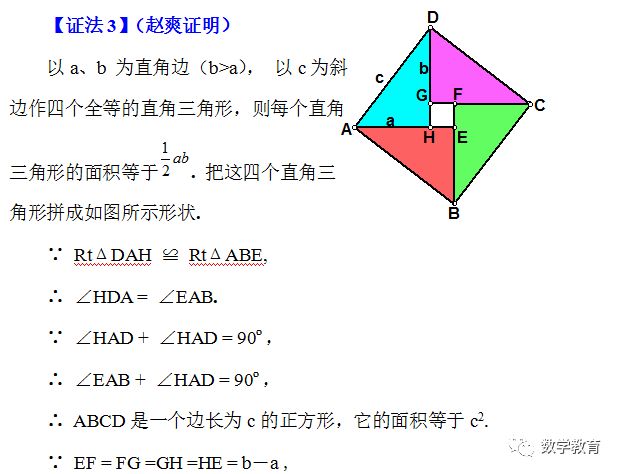
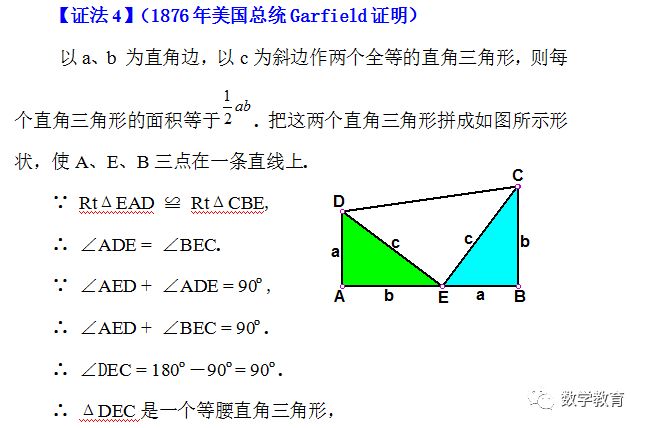

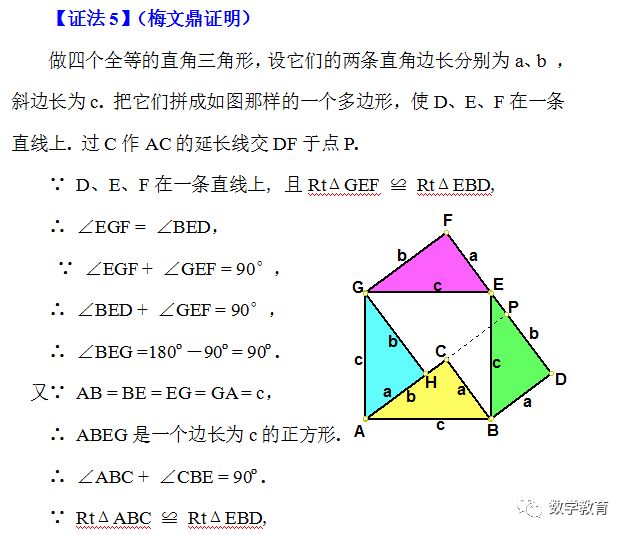

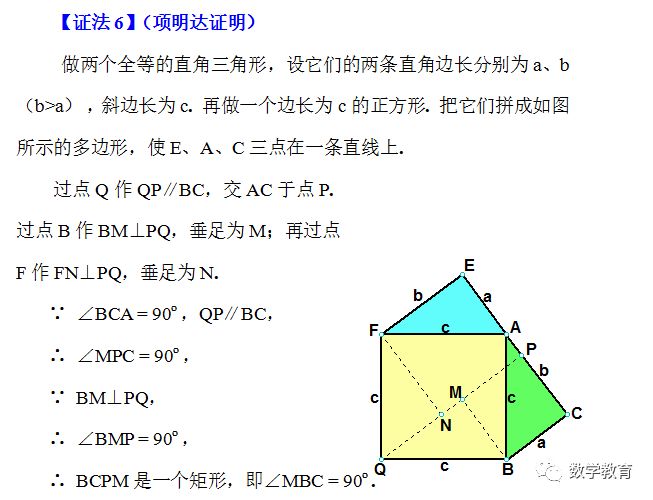

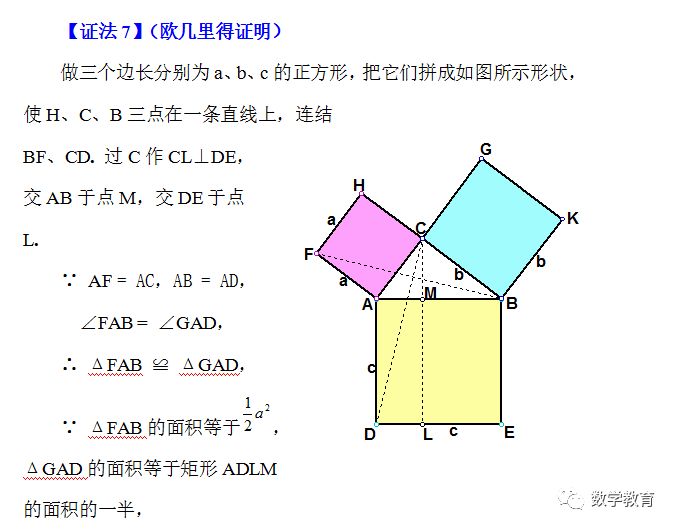

注:△GAD改为△CAD。
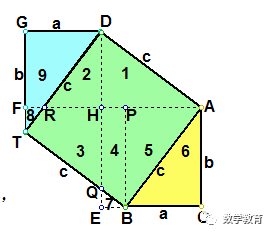
【证法9】(杨作玫证明)
做两个全等的直角三角形,设它们的两条直角边长分别为a、b(b>a),斜边长为c. 再做一个边长为c的正方形. 把它们拼成如图所示的多边形. 过A作AF⊥AC,AF交GT于F,AF交DT于R. 过B作BP⊥AF,垂足为P. 过D作DE与CB的延长线垂直,垂足为E,DE交AF于H.
∵ ∠BAD = 90o,∠PAC = 90o,
∴ ∠DAH = ∠BAC.
又∵ ∠DHA = 90o,∠BCA = 90o,AD = AB = c,
∴ RtΔDHA ≌ RtΔBCA.
∴ DH = BC = a,AH = AC = b.
由作法,PBCA 是一个矩形,所以 RtΔAPB ≌RtΔBCA.
即PB =CA = b,AP= a,从而PH = b―a.
∵ RtΔDGT ≌ RtΔBCA ,
RtΔDHA ≌ RtΔBCA.
∴ RtΔDGT ≌ RtΔDHA .
∴ DH = DG = a,∠GDT = ∠HDA .
又∵ ∠DGT = 90o,∠DHF = 90o,
∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90o,
∴ DGFH是一个边长为a的正方形.
∴ GF = FH = a . TF⊥AF,TF = GT―GF = b―a .
∴ TFPB是一个直角梯形,上底TF=b―a,下底BP= b,高FP=a +(b―a).
用数字表示面积的编号(如图),则以c为边长的正方形的面积为
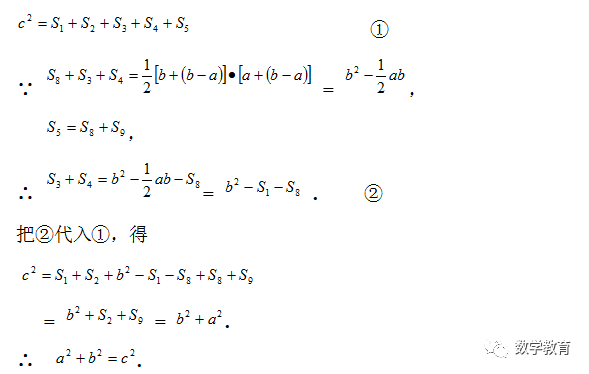
【证法10】(李锐证明)
设直角三角形两直角边的长分别为a、b(b>a),斜边的长为c. 做三个边长分别为a、b、c的正方形,把它们拼成如图所示形状,使A、E、G三点在一条直线上. 用数字表示面积的编号(如图).
∵ ∠TBE=∠ABH=90o,
∴ ∠TBH=∠ABE.
又∵ ∠BTH=∠BEA=90o,BT=BE=b,
∴RtΔHBT ≌RtΔABE.
∴HT=AE=a.
∴GH=GT―HT=b―a.
又∵ ∠GHF+∠BHT=90o,
∠DBC+∠BHT=∠TBH+∠BHT=90o,
∴∠GHF = ∠DBC.
∵ DB = EB―ED=b―a,∠HGF=∠BDC=90o,∴RtΔHGF ≌ RtΔBDC. 即 .
过Q作QM⊥AG,垂足是M. 由∠BAQ=∠BEA = 90o,
可知∠ABE=∠QAM,
而AB = AQ = c,所以RtΔABE ≌RtΔQAM .
又RtΔHBT ≌RtΔABE. 所以RtΔHBT ≌RtΔQAM .
由RtΔABE ≌RtΔQAM,
又得QM=AE=a,∠AQM=∠BAE.
∵ ∠AQM+∠FQM = 90o,∠BAE+∠CAR= 90o,
∠AQM=∠BAE,
∴∠FQM=∠CAR.
又∵ ∠QMF=∠ARC=90o,QM=AR=a,


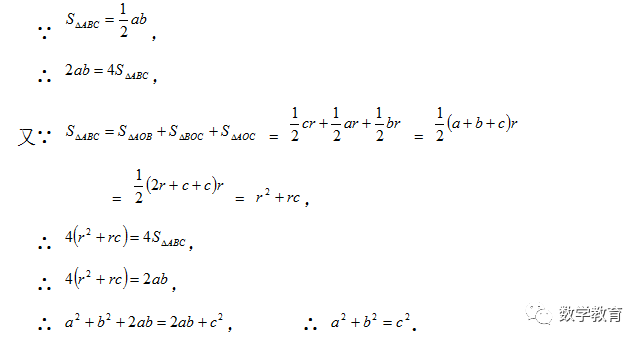


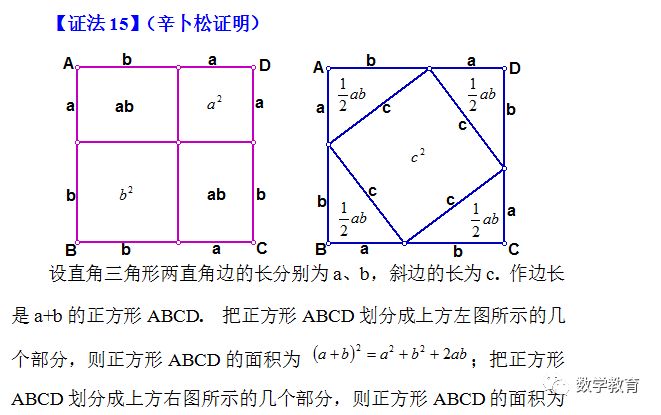
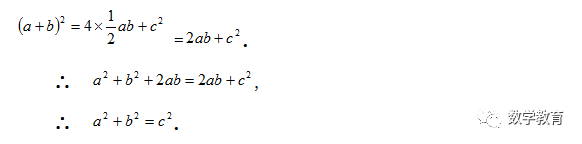
【证法16】(陈杰证明)
设直角三角形两直角边的长分别为a、b(b>a),斜边的长为c. 做两个边长分别为a、b的正方形(b>a),把它们拼成如图所示形状,使E、H、M三点在一条直线上. 用数字表示面积的编号(如图).
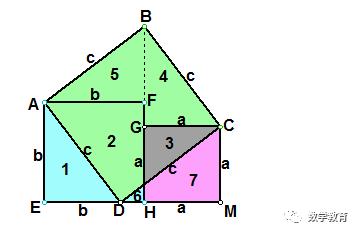
在EH=b上截取ED=a,连结DA、DC,则 AD=c.
∵EM=EH+HM=b+a , ED=a,
∴DM=EM―ED=-a=b.
又∵∠CMD=90o,CM=a,∠AED=90o, AE=b,
∴RtΔAED ≌RtΔDMC.
∴∠EAD=∠MDC,DC=AD=c.
∵∠ADE+∠ADC+∠MDC=180o,
∠ADE+∠MDC=∠ADE+∠EAD=90o,
∴∠ADC=90o.
∴作AB∥DC,CB∥DA,则ABCD是一个边长为c的正方形.
∵∠BAF+∠FAD=∠DAE +∠FAD=90o,
∴∠BAF=∠DAE.
连结FB,在ΔABF和ΔADE中,
∵AB=AD=c,AE=AF=b,∠BAF=∠DAE,
∴ΔABF ≌ΔADE.
∴∠AFB=∠AED=90o,BF=DE=a.
∴点B、F、G、H在一条直线上.
在RtΔABF和RtΔBCG中,
∵AB=BC=c,BF=CG=a,
∴RtΔABF ≌RtΔBCG.